10. Цапурин К.А. Местная потеря устойчивости при сжатии стандартного прессованного профиля, используемого в качестве стрингера

>> К списку публикаций >> К содержанию сборника

УДК 629.7.015.4:539.384.4

Цапурин К.А.

Научный руководитель – профессор Хазанов Х.С.

Рассматривается задача, в которой удлиненная пластинка нагружена в своей плоскости сжимающей нагрузкой, приложенной к коротким сторонам (рисунок 1). Длинные стороны имеют упругие на поворот опоры в виде примыкающих пластин. Предполагается, что нагруженные стороны свободно оперты.

Рисунок 1 – Сжатая пластинка

Инженерное решение поставленной задачи с учетом изложенных особенностей дано Ф.Блейхом в /1/ и широко используется в ракетно-авиационной технике /2/. Ф.Блейх обосновал применимость нижеследующего дифференциального уравнения изгиба пластины к исследованию ее устойчивости с учетом пластических деформаций:

(1)

где: m - коэффициент Пуассона в упругой области;

- цилиндрическая жесткость пластины;

- параметр, определяемый по диаграмме сжатия материала;

E_k - касательный модуль, Е – модуль упругости материала.

Интегрирование дифференциального уравнения (1) при свободном опирании по нагруженным краям и упругой заделке пластины по боковым кромкам приводит к следующей формуле (при аb, m = 0.3):

, (2)

где k – коэффициент устойчивости.

В /1,2/ даются формулы для определения этого коэффициента применительно к сжатым профилям, образованным из пластин, сходящихся под прямым углом.

Формулу (2) можно привести к виду

(3)

Величина представляет собой критическое напряжение, подсчитываемое при условии, что потеря устойчивости имеет место в пределах пропорциональности (t = 1). Величина s ^*_кр находилась с применением МКЭ–пакета программ MSC / PATRAN / NASTRAN. Использовались четырехузловые оболочечные конечные элементы с шестью степенями свободы в каждом узле. Напряжение s ^*_кр определялось из решения обобщенной проблемы собственных значений.

Используя диаграмму сжатия для материала АМГ6, построен по методике Ф.Блейха вспомогательный график , приведенный на рисунке 2.

Рисунок 2 – Вспомогательный график

По графику находятся критические напряжения с учетом пластических деформаций по найденным значениям s ^*_кр.

Рассмотрим профиль № 540818, нагруженный распределенными сжимающими силами и имеющий свободное опирание по торцам. На рисунке 3 показана форма его поперечного сечения. Результаты расчетов для профиля, имеющего различную длину, приведены в таблице 1.

Рисунок 3 - Форма поперечного сечения профиля

Таблица 1 - Значение s ^*_кр при расчете профиля по МКЭ для различной длины модели

Из таблицы 1 видно, что с увеличением длины модели, критические напряжения уменьшаются, и они значительно выше предела пропорциональности (для АМГ6 s _пц = 130 МПа). С помощью графика (рис. 2) определим критические напряжения с учетом пластических деформаций (таблица 2).

Таблица 2 - Значение s _кр при расчете профиля по МКЭ для различной длины модели

На рисунке 4 показана местная форма потери устойчивости профиля длиной 160 мм. Видно, что потеряла устойчивость полочка стрингера. Форма местной потери устойчивости полочки получается такая же, как и при сжатой пластине, свободно опертой по трем сторонам.

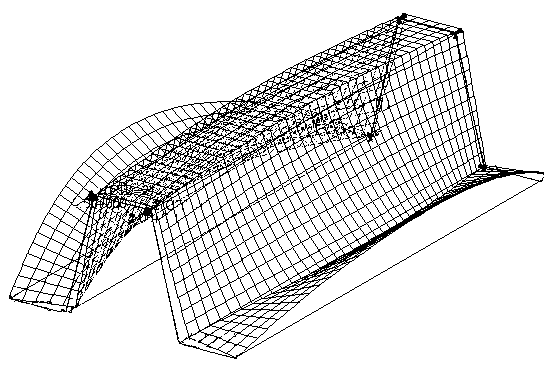
Рисунок 4 – Форма потери устойчивости полочки профиля

Рассмотрим стрингер с приваренной к нему полосой обшивки (рис. 5). По линии сварки (штриховые линии) узлы конечных элементов стрингера и обшивки сливаются. Размер конечных элементов 4х4 мм. Минимальная толщина обшивки (4,1 мм) выбрана из тех соображений, чтобы она не теряла устойчивость раньше элементов стрингера.

Рисунок 5 - Обшивка, подкреплённая стрингером

Результаты расчетов приведены в таблице 3, из которой следует, что значение s ^*_кр с увеличением длины конструкции остается практически неизменным.

Таблица 3 - Значения s ^*_кр при расчете стрингера с обшивкой по МКЭ

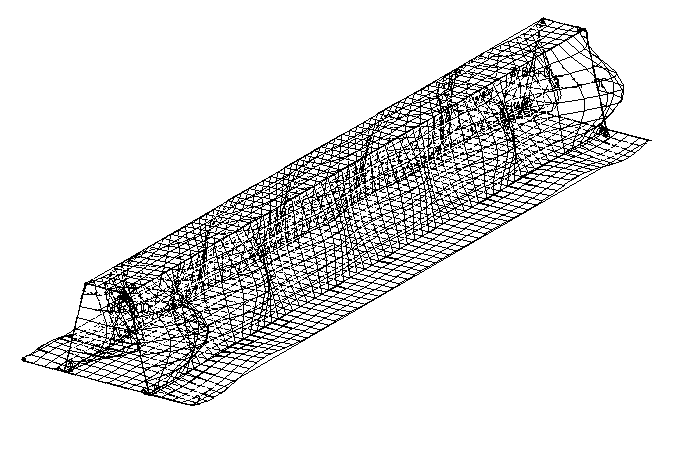
Рисунок 6 – Форма потери устойчивости стрингера с обшивкой

По графику (рис. 2) определены критические напряжения с учетом пластических деформаций, которые равны 210 МПА.

На рисунке 6 показана местная форма потери устойчивости конструкции. Видно, что потеряли устойчивость боковые (тонкие и длинные) стороны стрингера. Заметно, что они существенно выпучиваются лишь у торцов балки, а средняя часть остается почти плоской. Это совершенно не похоже на формы потери устойчивости, известные для сжатых пластин.

Упростим ранее исследуемую задачу (стрингер с обшивкой). Рассмотрим модель с поперечным сечением, изображённым на рисунке 7, в которой отсутствуют полки стрингера и часть обшивки вне контура стрингера. Значения s ^*_кр, полученные по МКЭ для различных длин, приведены в таблице 4.

Рисунок 7 - Форма поперечного сечения

Таблица 4 - Значения s ^*_кр при расчёте упрощенной модели по МКЭ

Сопоставление результатов, приведенных в таблицах 3 и 4, показывает, что они отличаются друг от друга всего лишь на 2,3…2,4 %. Таким образом, в практических расчетах местной потери устойчивости стрингера с обшивкой можно пользоваться упрощенной моделью, показанной на рисунке 7.

СПИСОК ЛИТЕРАТУРЫ

1. Блейх Ф. Устойчивость металлических конструкций – М.: ОГИЗ, 1959.–544 с.
2. Моссаковский В.И. и др., Прочность ракетных конструкций: Учеб. пособие для авиацион. спец. вузов .;Под ред. В.И. Моссаковского.– М.: Высш. шк., 1990.– 359 с.